11320. Amazing trick
Alice is a magician, and she creates a new
trick. She has n cards with different numbers
from 1 to n written on them. First, she asks an
audience member to shuffle the deck and put the cards in a row. Let the number
on the i-th card from the left be ai.
Then Alice selects two permutations p and
q. There is a restriction on p and q: permutations can’t
have fixed points. In other words, ∀i: pi ≠ i and qi ≠ i.
Once the permutations are chosen, Alice
shuffles the cards according to them. Now the i-th card from the left becomes
the card a[p[q[i]]. The trick is considered
successful if, after shuffling, the number on the i-th card from the left
is i.
Help Alice choose the permutations p and q,
or determine if it is impossible for the given starting permutation a.
Input. The first line contains the number of test cases t (1
≤ t ≤ 105).
Each test is described in two lines. The
first line contains one integer n (1 ≤ n ≤ 105) – the
number of cards. The second line contains n integers ai (1 ≤ ai ≤ n, ∀i ≠ j: ai ≠ aj)
– the initial permutation of the cards.
It is guaranteed that the sum of n over
all tests does not exceed 105.
Output. Print the answer for each test case in the order they
appear in the input.
For each test case, print “Impossible” on a
single line if no solution exists.
Otherwise, print “Possible” on the first
line, followed by two lines containing the permutations p and q.
|
Sample
input |
Sample
output |
|
4 2 2 1 3 1 2 3 4 2 1 4 3 5 5 1 4 2 3 |
Impossible Possible 3 1 2 2 3 1 Possible 3 4 2 1 3 4 2 1 Possible 4 1 2 5 3 3 1 4 5 2 |
SOLUTION
combinatorics
Algorithm
analysis
Let’s consider three permutations: a,
p, and q. Let I be the identity permutation. Consider the
equation: a(p(q( I ))) =
I. From this, we get p(q( I )) = a-1.
Using the fact that permutations are applied from right to left, this identity
can be rewritten as: p °
q = a-1. Therefore, q = p-1 ° a-1.
Generate a random permutation p that
has no fixed points. Then, compute the permutation q = p-1 °
a-1 and check that it has no fixed
points. The found permutations p and q are the required ones.
Example
Consider
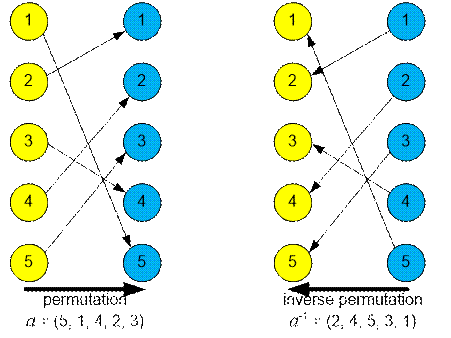
the permutation a
= (5, 1, 4, 2, 3).
Its
inverse will be a-1 = (2, 4, 5, 3, 1).
Generate
a random permutation p with no fixed points. For example, let p = (4, 1, 2, 5, 3).
Now, let’s compute its inverse: p-1 = (2, 3, 5, 1, 4).
Next,
compute q = p-1 °
a-1 = (2, 3, 5, 1, 4) ° (2, 4, 5, 3, 1) = (3,
1, 4, 5, 2). The permutation q has no fixed points, so it is
valid.
Algorithm implementation
The
print function prints the elements of the array a,
starting from the first one.
void print(vector<int>& a)
{
for (int i = 1; i < a.size(); i++)
printf("%d ", a[i]);
printf("\n");
}
The
function is_valid checks whether the permutation v
contains any fixed points.
bool is_valid(vector<int>& v)
{
for (int i = 1; i < v.size(); i++)
if (v[i] == i) return false;
return true;
}
Declare
the arrays.
vector<int> a, p, p1, q;
The
main part of the program. Read the input data.
scanf("%d", &tests);
while (tests--)
{
scanf("%d", &n);
Initialize
the arrays.
a.resize(n + 1);
p1.resize(n + 1);
p.resize(n + 1);
q.resize(n + 1);
Read
the input permutation a and immediately store its inverse in the array a.
That is, the array a contains the permutation a-1, where a is the input
permutation.
for (i = 1; i <= n; i++)
{
scanf("%d", &x);
a[x] = i;
}
mt19937
is one of the standard pseudorandom number generators in C++ (Mersenne Twister
with a period of 19937). It is very fast and has good statistical properties,
making it an excellent choice for most tasks requiring random number
generation.
mt19937 gen(random_device{}());
In the variable found, we’ll mark whether a
solution is found for the current test.
found = false;
Perform 1000 iterations.
for (it = 0; it < 1000;
it++)
{
Generate a random permutation. To do this, populate the
array p with the numbers 0, 1, 2, …, and use the shuffle
function to shuffle the elements, starting from the first (non-zero) element. We
work with permutations from 1 to n.
iota(p.begin(), p.end(), 0);
shuffle(p.begin() + 1, p.end(), gen);
Check whether the permutation p is valid (i.e., it
contains no fixed points).
if (!is_valid(p)) continue;
Compute the permutation p1 = p-1.
for (i = 1; i <= n; i++)
p1[p[i]] = i;
Compute the permutation q = p1
° a-1 = p-1 °
a-1.
for (i = 1; i <= n; i++)
q[i] = p1[a[i]];
If the permutation q is valid, print the result.
if (is_valid(q))
{
puts("Possible");
print(p);
print(q);
found = true;
break;
}
}
If no solution is found after 1000 iterations, then no
solution exists.
if (!found) puts("Impossible");
}